Raspberry Pi で制御するラズドローンの製作記録(2)

トイドローンTelloを楽しんで、ドローンキットRoboCat270を組立て、試験飛行することで、ドローンの仕組みを理解することができた。(RoboCat270の記録はここ)
これから綴るのは、Raspberry Piで制御するドローン、ラズドローンを製作した記録。
●Raspberry Piをどのように使うか
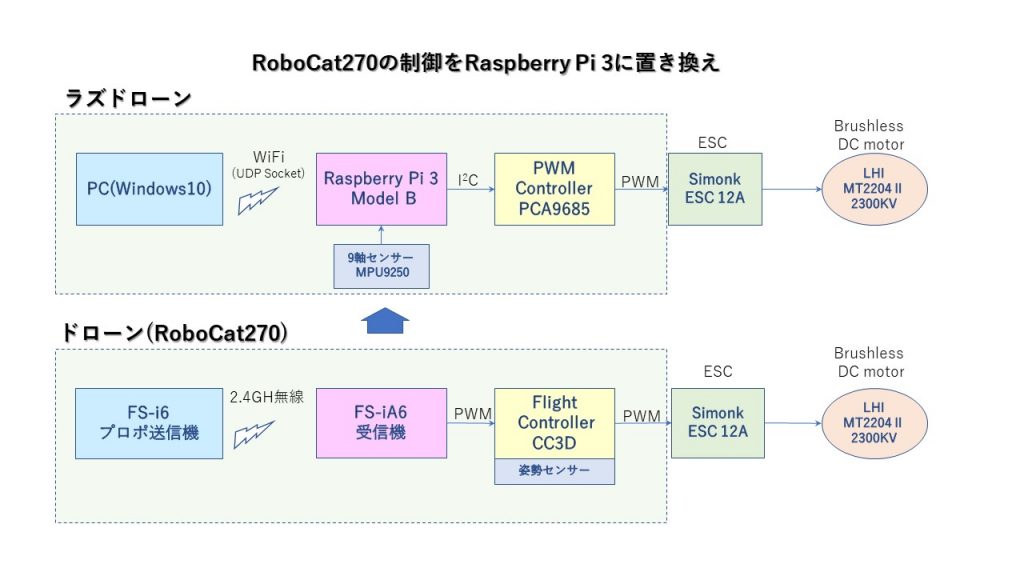
完成したRoboCat270のFC(Flight Controller:CC3D、姿勢センサー付き)と受信機を、Raspberry Piに置き換え、姿勢センサーは9軸センサー(MPU9250)を使うこととした。プロポ送受信機の代わりに、PC(Windows10)でGUI操作プログラムを作って、WiFiでRaspberry Piに制御信号を送ることとした。室内で飛行することを断念し、GPS、気圧センサーなどは付けず、この組み合わせで、プロペラが回り、PID制御で浮上するところまでできれば完成とした。
●Raspberry Piを使ったラズドローンの部品構成はこのようになる
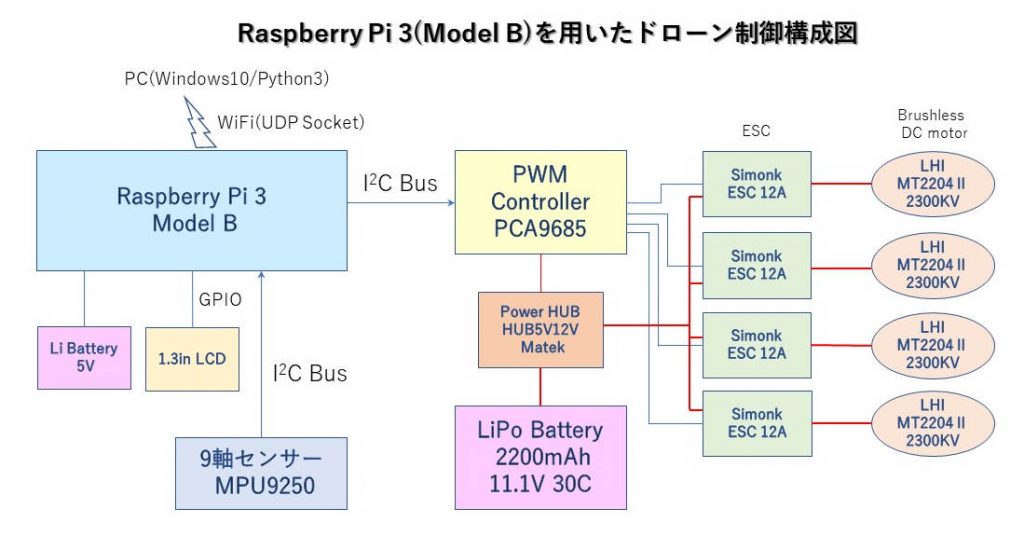
PCからの操作指令をWiFiでRaspberry Piに飛ばし、その指令データをRaspberry Piで解釈し、PWMコントローラー(PCA9685)にPWM発生信号を送り、モーターを回転させる。ラズドローンの姿勢は、MPU-9250の9軸センサーの加速度、ジャイロデータから傾きを計算し、水平になるように、PID制御により各軸のモーター回転数を制御する。
バッテリーは、LiPoバッテリー(2200mAh,11.1V,30C)を用い、PowerHUBを通して、モーター用の12V,制御用の5Vを取り入れた。Raspberry Pi用の電源として、モーター電源とは切り離し、スマホ充電Liバッテリー(5V, 3000mAh)を用いた。データ確認のためRaspberry Piには1.3inのLCDを搭載したが、モーターが回転している時には危険で近づけず、有効な手段ではなかった。プログラムの動きは、PCリモート操作のVNCで確認することにした。
<追加の部品リスト>
MPU-9250 9軸センサモジュール(3軸加速度+3軸ジャイロ+3軸コンパス)
(\2,000 : ストロベリー・リナックス)
1.3インチIPS OLED LCDディスプレイスクリーンHAT(\2,199 : Amazon)
I2C接続16チャンネル サーボ&PWM駆動キット(PCA9685)(\950 : 秋月電子通商)
●ラズドローンの組立

RoboCat270のフレーム3階の受信機とFCを取り外し、アクリル板4枚を積層してRasPi 関連の部品を取り付けた。アクリル板1階には、RasPiの電源となるスマホ充電バッテリー(3000mAh)をマジックテープで取り付け。2階には、PWM Controller(PCA8685)とRaspberry Pi 3Bをプラネジで固定。3階には、9軸センサーと1.3in LCD HATをプラネジで固定した。
●ラズドローンのプログラム構成
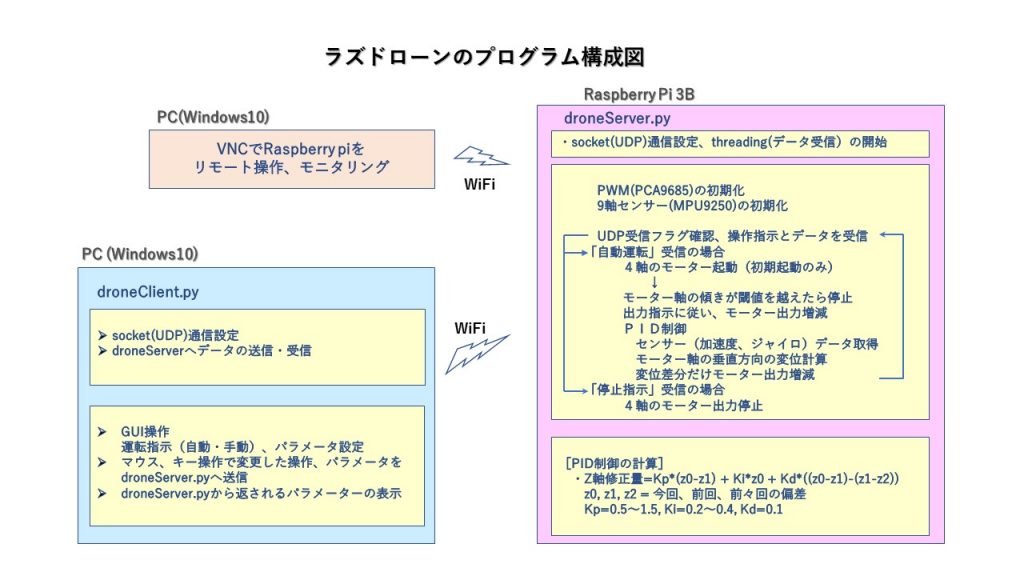
ケーブル類は接続できないので、Raspberry PiをWiFiでPC(Windows10)と接続して、VNCでリモート操作。ラズドローンの操作指示はPC(pythonプログラム)で行っている。PCとRaspberry Piはsocket(UDP)接続して、PCから送信される操作指示(自動・手動・停止、パラメーター)をRaspberry Piで受信して、処理をしている。
・センサーデータからモーター軸の変位計算
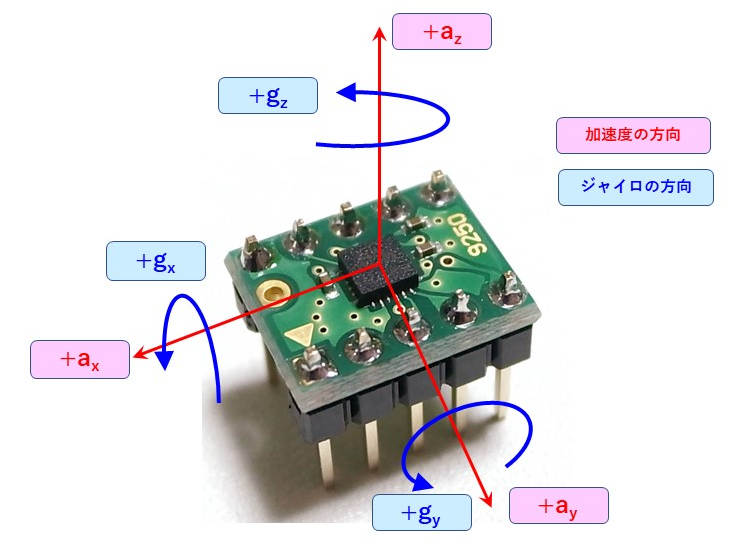
ジャイロセンサーからは、\(X, Y, Z\)軸周りの回転角速度\(g_{x}, g_{y}, g_{z}(deg/sec)\)が得られるので、時間で積分すれば、時間\(t\)の時の各軸周りの回転角度\(G_{x}, G_{y}, G_{z} (deg)\)が計算できる。
\(G_{x} = \displaystyle \int_0^t g_{x}(t) dt\) \(G_{y}(t), G_{z}(t)\)も同様
プログラムの中では、\(\Delta t\)間隔で回転角速度をサンプリングして、\(\Large \Sigma\)をとっている。
\(G_{x} = \displaystyle \frac{1}{2}\displaystyle \sum_{i=1}^{n} (g_{x}(i) + g_{x}(i – 1)) \times \Delta t \)
加速度センサーからは、\(X,Y,Z\)軸方向の重力加速度\(a_{x}, a_{y}, a_{z} (g)\)が得られるので、その時点での各軸の回転角\(A_{x}, A_{y}, A_{z} (rad)\)が計算できる。
\(A_{x} = \tan^{-1} \left(\frac{\Large a_{y}}{\sqrt{\Large {a_{x}}^{2} + \Large {a_{z}}^{2}}}\right)\)
\(A_{y} = \tan^{-1} \left(\frac{\Large – a_{x}}{\sqrt{\Large {a_{y}}^{2} + \Large {a_{z}}^{2}}}\right)\)
\(A_{z} = \tan^{-1} \left(\frac{\sqrt{\Large {a_{x}}^{2} + \Large {a_{y}}^{2}}}{\Large a_{z}}\right)\)
この2つの回転角度\(G, A\)に重みを付けて、単位を\(rad\)に統一して、各軸の回転角\({\theta}_{x}, {\theta}_{y}, {\theta}_{z}\)を得た。
\({\theta}_{x} = k_{1} \times G_{x} + k_{2} \times A_{x}\)
\({\theta}_{y} = k_{1} \times G_{y} + k_{2} \times A_{y}\)
\({\theta}_{z} = G_{z}\)
\(k_{1} = 0.95, k_{2} = 0.05\) とした。
水平時のモータ軸の位置座標を\(P_{0} = (p_{x0}, p_{y0}, p_{z0})\)として、\(X\)軸、\(Y\)軸、\(Z\)軸周りに、それぞれ\(\theta_{x}, \theta_{y}, \theta_{z}\)回転した後のモータ軸位置座標\(P = (p_{x}, p_{y}, p_{z})\)を求め、\(Z\)軸方向の変位\(p_{z}\)を監視する。
この計算式を用いて、ラズドローンの動きをディスプレイに3次元座標で表示し確認した。
ラズドローンの動きに3D画像がほぼ追随していることが分かる。
●PID制御のプログラム
・Roll角、Pitch角を制御する方法
ある時間におけるRoll角\(\theta_{x}\)、Pitch角\(\theta_{y}\)が得られるので、それぞれの角度偏差が\(0\)(ゼロ)になるよう、PID制御で4軸のモーターの出力を増減させる。今回、Yaw角\(\theta_{z}\)はジャイロからしか取得できず、正確なデータが得られないことと、浮上試験にはあまり影響しないので、取り扱わないこととした。ある時間における操作量\(MV_{n}\)は次の様にして得ることができる。角度偏差からモーターの操作量を決めるのは難しいが、偏差操作1.0\((deg)\)に対して、モーター出力0.35%相当とした。
\(MV_{n} = MV_{n-1} + \Delta MV_{n}\)
\(\Delta MV_{n} = K_{p} \times\) 偏差 \(+ K_{i} \times\)偏差の累積値 \(+K_{d} \times\) 前回偏差との差
(比例項) (積分項) (微分項)
\(= K_{p} \times (e_{n} – e_{n-1}) + K_{i} \times e_{n} + K_{d} \times{(e_{n} – e_{n-1}) – (e_{n-1} – e_{n-2})}\)
ここで、
\(MV_{n}, MV_{n-1}\):今回、前回の操作量
\(\Delta MV_{n}\):今回の操作量差分
\(e_{n}, e_{n-1}, e_{n-2}\):今回、前回、前々回の偏差
\(K_{p} = 0.5 \sim 1.5, K_{i} = 0.2 \sim 0.4, K_{d} = 0.1\)
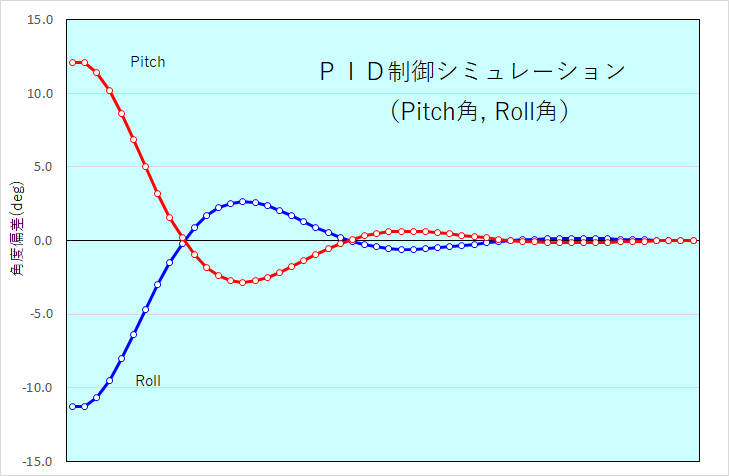
・Roll角、Pitch角のPID制御シミュレーション
初期偏差\(\theta x = -11.3, \theta y = 12.1\)でシミュレーションした結果を示します。このシミュレーションでは収束に時間がかかっているように見えるが、分かりやすくするため応答速度を少し遅くしているため。ここで使ったパラメータは、\(K_{p} = 1.0, K_{i} = 0.3, K_{d}= 0.1\)。
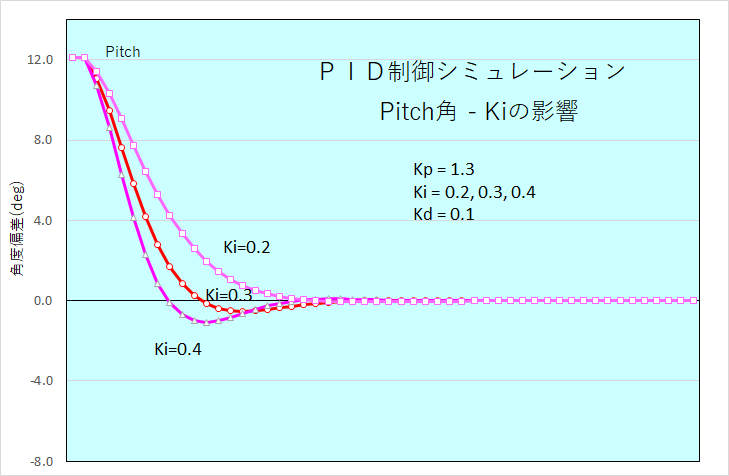
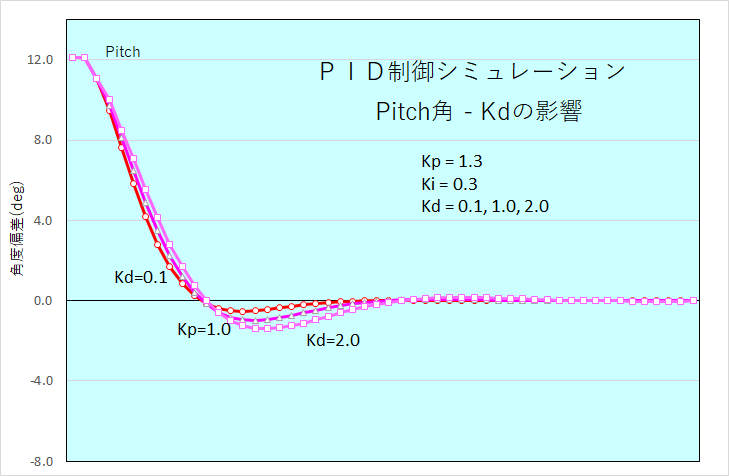
・パラメータKp, Ki, Kdの効果
パラメータKp, Ki, Kdを変化させてシミュレーション計算した結果、Kpの効果が一番大きく、Kdは変化させてもあまり変わらない。

・モーターの垂直(Z)軸の偏差を制御する方法
ラズドローンのモーター4軸の水平面からの傾き、すなわち垂直Z軸方向の偏差\(Z_{i} (i = 1 \sim 4)\)がセンサーから座標変換を行って得られるので、その偏差を0にするように、モーター出力を増減させる。実際には、3つのモーター軸の偏差、\(Z_{1}, Z_{2}, Z_{3}\)が0になるように制御すれば、姿勢を水平に保てる。PIDの求め方は、Roll角度の偏差の時と同じだが、Z軸偏差操作1.0mmに対して、モーター出力0.25%相当とした。
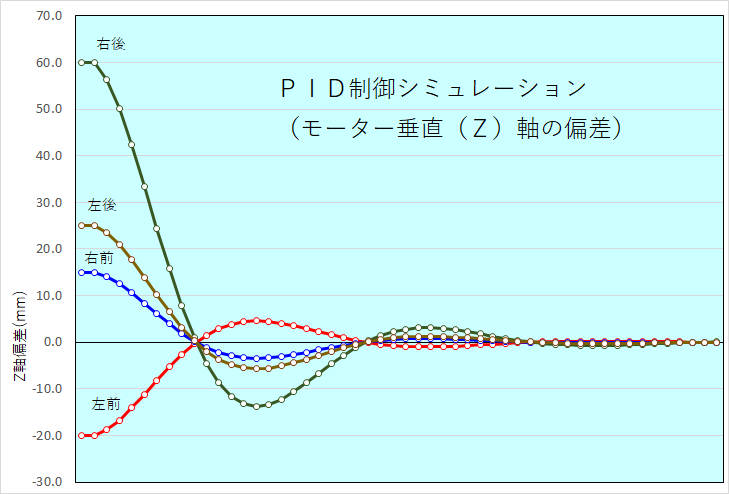
・モーターの垂直(Z)軸のPID制御シミュレーション
初期偏差\(Z_{1} = -20.0\)(左前), \(Z_{2} = +15.0\)(右前), \(Z_{3} = +60.0\)(右後), \(Z_{4} = +25.0\)(左後)でシミュレーションした結果を示します。Roll角と同じく、収束に時間がかかっているように見えるのは応答速度を少し遅くしているため。ここで使ったパラメータは、\(K_{p} = 1.0, K_{i} = 0.3, K_{d} = 0.1\)。
●ESCへ送るPWM信号の仕様
RoboCat270のFC(Flight Controller)から出力される波形をオシロスコープで測定し、PWM周波数=400Hz、Duty比=0.4~0.8(出力0%~100%)を使っていることが分かった。この設定値をそのままPWM Controller(PCA-9685)にも使うことにした。尚、インターナルクロックは25MHzとした。
●ESCのキャリブレーション
4軸のモーターを個別に初期化。PWMのDuty比0.8(出力100%)に設定して、バッテリーを接続し、「ピー、ピー」という音でスロットルのトップポイントを設定。2秒以内に出力0%(Duty0.5)に戻すと、長めの「ピーー」という音で、ボトムポイントが設定される。
モーターの回転数は非接触レーザータコメータFMTDT2234C(\1,850 Amazon)で測定した。4つのモーターには若干の個体差があり、起動開始のPWMデューティ比は異なるので、それはキャリブレーション補正値として記憶した。また同じ出力レベルでも、回転数に5%程度の差がある。

●モーターの出力調整
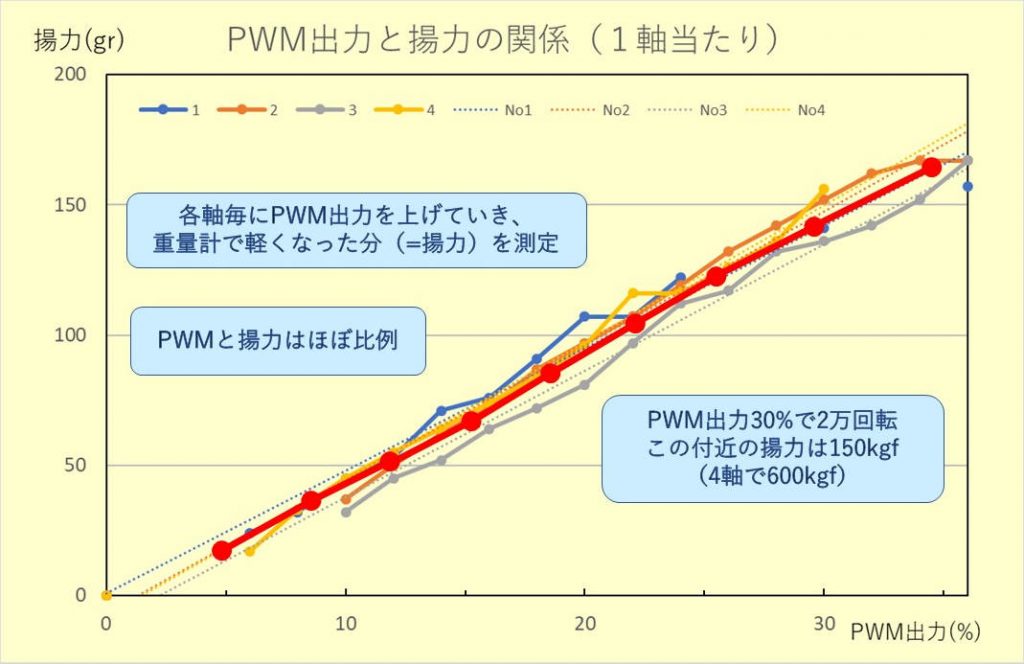
プロペラの回転数に対する揚力を計るために、ラズドローンを1.1kgfの錘に固定して、重量計りに載せて、揚力を測定した。プロペラを回転させて、重量計りの重さが軽くなった分が揚力。

PWM出力と揚力はほぼ比例し、PWM出力30%付近でモーター回転数が2万回転となり、揚力は150kgf(1軸当たり)、4軸で600kgfとなる。4軸同時に回転させると、各軸の揚力を足した以上の揚力が得られるので、ドローンの重量780kgfを浮上させることができる。
●完成したラズドローンの浮上試験

室内で2万回転のプロペラは凶器と同じ。暴走しないようにユニバーサルジョイントである程度自由度を持たせながら固定した。センサーパラメータや、PIDパラメータの設定が悪く、何度も転倒を繰り返し、試行錯誤の中で、少しではあるが浮上した。
PID制御の方法をもう少し追求しなければ、この試験は成功したと言えない。これで飛行できるとは思わないが、高回転のプロペラは危険で、これ以上、家の中で試験を続けて行くのは止めることとした。プロペラを回さず、PID制御を検証する方法を考えて、再チャレンジする。




