Si5351A I2Cクロックジェネレーターを使った周波数波形出力プログラム例

Silicon Laboratories社製Si5351Aを使用したクロックジェネレーターモジュール（ここではストロベリーリナックス社）を使い、Raspberry Piで電波時計用の40kHz/60kHzの周波数の長波を出すプログラム例を紹介する。

このモジュールは、I2C制御で個別設定できる3chの端子からそれぞれ2.5kHz～200MHzの任意の周波数を出力することができる。原発振は25MHzの水晶で、内部VCOとPLLをI2C制御することで逓倍かつ分周し任意の周波数を発生させる。

●使用したハードウェア

Si5351A I2Cクロックジェネレータモジュール
\990(ストロベリーリナックス社)※秋月電子通商製もあるが、在庫なしで入手できなかった

■主な仕様
　・ジェネレータ： Si5351A（Silicon Laboratories）
　・出力範囲：2.5kHz～200MHzまで
　・出力波形：方形波のみ
　・出力数：3ch
　・原発振：25MHz水晶
　・コア電圧：2.5V～3.6V
　・ロジック電圧：1.8V～3.6V
　・出力レベル：1.8V～3.6VのLVTTL

●Raspberry Pi とクロックジェネレーターモジュールの接続

●任意の周波数の発生方法

　Si5351には３タイプあり、このモジュールに使用されているのはSi5351Aで、原発振は水晶発振だけとなっている。このデバイスは２つのPLL(PLLA/PLLB)から構成されていて、それぞれのPLLは600～900MHz範囲の中間VCO周波数を発生させるフィードバックMultisynthから構成されている。２つのVCO周波数はMultisynth dividerによって、500kHz～200MHzのMultisynth周波数を発生させる。更にR dividersで周波数を2.5kHzまで下げることができる。

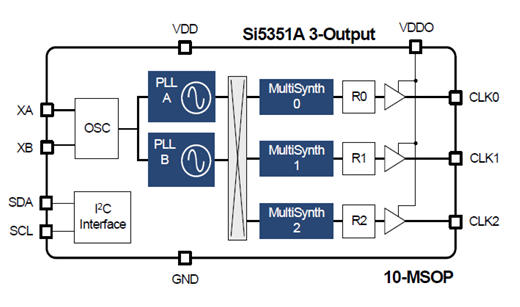
以降、簡単化するために、PLLAから中間周波数\(f_{vco}\)を出力、Multisynth0、R0を使い、CLK0から出力周波数\(f_{out}\)を出力するための計算式を示す。

(1)中間周波数\(f_{vco}\)を出力するレジスター・パラメーターの設定
　　\(f_{vco} = f_{XTAL} \times Fr\)
　　　　\(f_{XTAL} = 25MHz\) : このモジュールのクリスタル周波数
　　　　\(Fr\) : Fractional Ratio

　　\(Fr(Fractional Ratio)\)は次のように算出する。
　　\(Fr = \displaystyle (a + \frac{b}{c})\displaystyle\)
　　　　\(a : 15 ～ 90\)
　　　　\(b : 0 ～ 1,048,575\)
　　　　\(c : 1 ～ 1,048,575\)

　　ここで得られた\(a,b,c\)を用いて、レジスター26 ～ 33のパラメータMSNA_P1, MSNA_P2, MSNA_P3を算出する
　　MSNA_P1 [17:0]= \(\displaystyle 128 \times a + Floor(128 \times \frac{b}{c}) -512\displaystyle \)
　　MSNA_P2 [19:0]= \(\displaystyle 128 \times b – c \times Floor(128 \times \frac{b}{c})\displaystyle \)
　　MSNA_P3 [19:0]= \(c\)

(2) 出力周波数\(f_{out}\)を出力するレジスター・パラメーターの設定（\(f_{out} <= 150MHz\)の場合）
　　\( f_{out} = \displaystyle (\frac{f_{vco}}{Multisynth \times R})\displaystyle\)
　　　　\(f_{out}\) : 出力周波数、500kHz ～ 200MHz
　　　　　　\(R\)(Divide Ratio)を使うと、500kHz以下の周波数を発生させることができる。
　　　　\(f_{vco}\) : 中間のVCO周波数
　　　　\(Multisynth\) : Multisynth Divider Ratio
　　　　\(R\) : Divide Ratio = 1, 2, 4, 8, 16, 32, 64, 128（500kHz以下の時）

　　\(Multisynth\) (Multisynth Divider Ratio)は、次のように算出する。
　　\(Multisynth = A + \displaystyle\frac{B}{C}\displaystyle\)、この結果は 6 ～ 1800の範囲でなければならない。
　　　　\(A : 15 ～ 90\)
　　　　\(B : 0 ～ 1,048,575\)
　　　　\(C : 1 ～ 1,048,575\)

　　ここで得られた、\(A,B,C\)を用いて、レジスター42 ～ 49のパラメータMS0_P1, MS0_P2, MS0_P3と、レジスター44のR0_DIVを算出する。
　　MS0_P1 [17:0]= \(\displaystyle 128 \times A + Floor(128 \times \frac{B}{C}) -512\displaystyle \)
　　MS0_P2 [19:0]= \(\displaystyle 128 \times B – C \times Floor(128 \times \frac{B}{C})\displaystyle \)
　　MS0_P3 [19:0]= \(C\)
　　R0_DIV[2:0] = \(R\)

●具体的事例でのレジスター設定

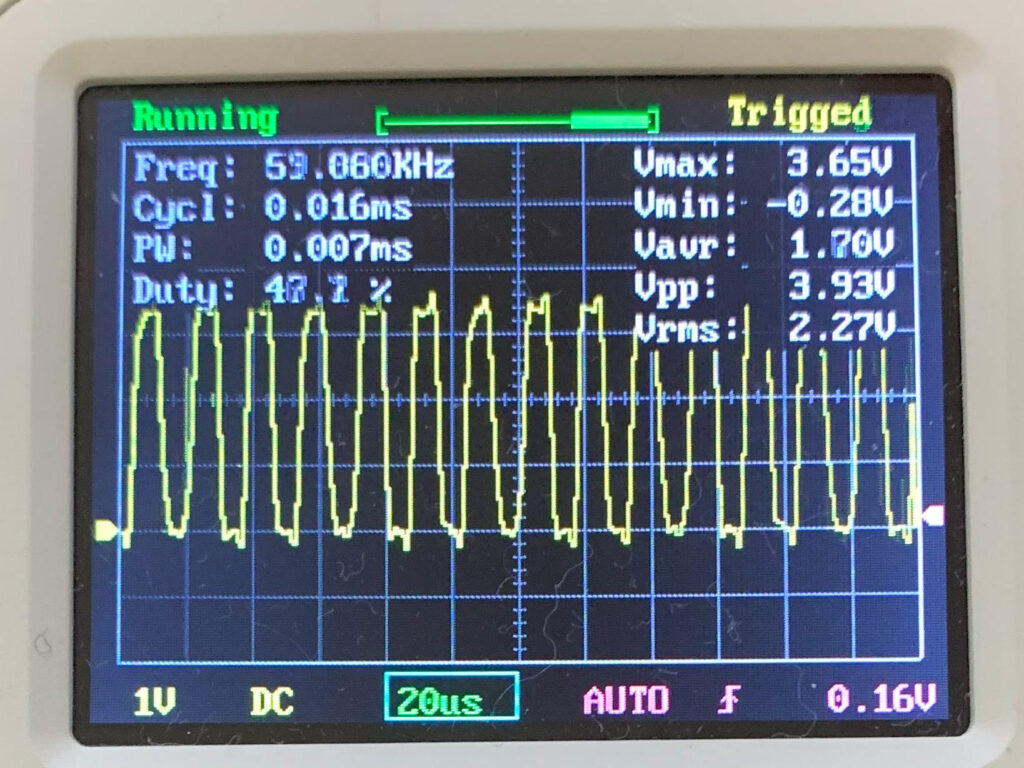
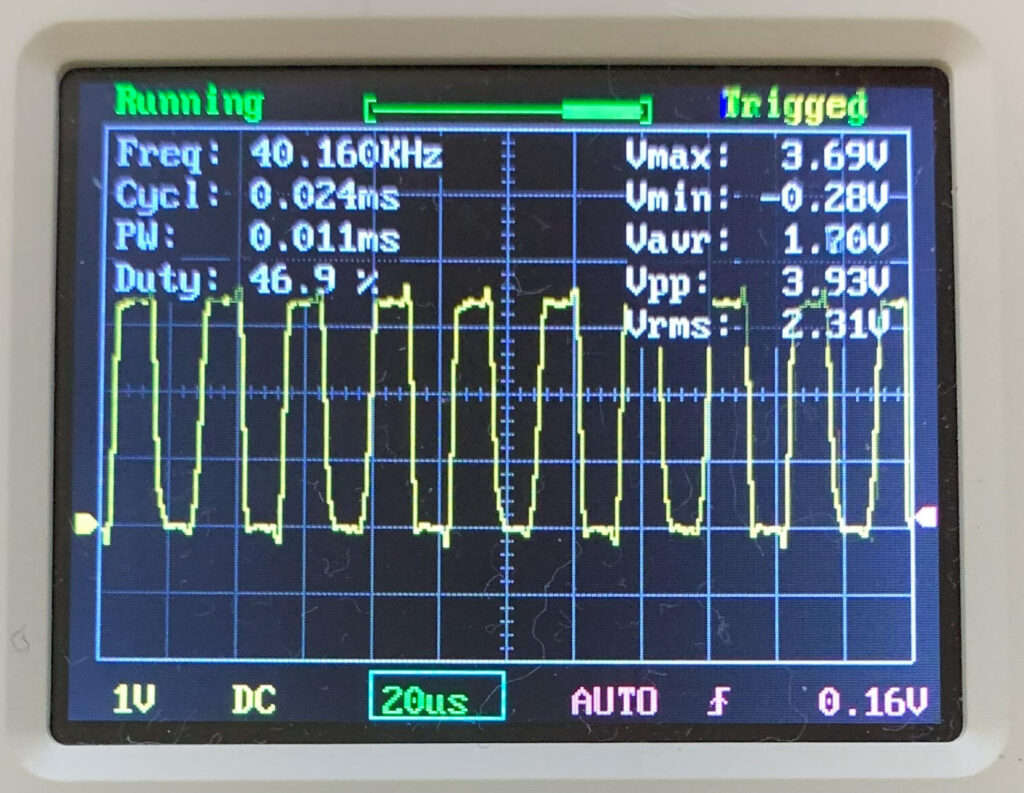
電波時計の受信/送信周波数は、40kHz(東)と60kHz（西）なので、その２つの周波数を出力するレジスターパラメータを計算する。

＜40kHz＞
　　\(f_{vco} = 25,000kHz \times 16 = 400,000kHz\)
　　　\(a = 15, b = 1, c = 1　→　\displaystyle a + \frac{b}{c}\displaystyle = 16\)
　　MSNA_P1 [17:0]= \(\displaystyle128 \times 15 + Floor(128 \times \frac{1}{1}) – 512 \displaystyle\)= 1536(0x600)
　　MSNA_P2 [19:0]= \(\displaystyle128 \times 1 – 1 \times Floor(128 \times \frac{1}{1})\displaystyle\) = 0
　　MSNA_P3 [19:0]= 1
　　\(f_{out} =\displaystyle\frac{400,000kHz}{1250 \times 8}\displaystyle = 40kHz\)
　　　\(A = 50, B = 1200, C = 1 → 　A + \displaystyle\frac{B}{C} = 16\displaystyle\)
　　　\(R = 8\)
　　MS0_P1 [17:0]= \(\displaystyle128 \times 50 + Floor(128 \times \frac{1200}{1}) -512\displaystyle\) = 159,488(0x26F00)
　　MS0_P2 [19:0]= \(\displaystyle128 \times 1200 – 1 \times Floor(128 \times \frac{1200}{1})\displaystyle\) = 0
　　MS0_P3 [19:0]= 1
　　R0_DIV[2:0] = 011b（Divide by 8の場合、\(2^3\)）

＜60kHz＞
　　\(f_{vco} = 25,000kHz \times 24 = 600,000kHz\)
　　　\(a = 23, b = 1, c = 1　→　\displaystyle a + \frac{b}{c}\displaystyle = 24\)
　　MSNA_P1 [17:0]= \(\displaystyle128 \times 23 + Floor(128 \times \frac{1}{1}) -512\displaystyle\) = 2560(0xA00)
　　MSNA_P2 [19:0]= \(\displaystyle128 \times 1 – 1 \times Floor(128 \times \frac{1}{1})\displaystyle\) = 0
　　MSNA_P3 [19:0]= 1
　　\(f_{out} =\displaystyle\frac{600,000kHz}{1250 \times 8}\displaystyle = 60kHz\)
　　　\(A = 50, B = 1200, C = 1 → 　\displaystyle A + \frac{B}{C}\displaystyle = 16\)
　　　\(R = 8\)
　　MS0_P1 [17:0]= \(\displaystyle128 \times 50 + Floor(128 \times \frac{1200}{1}) -512\displaystyle\) = 159,488(0x26F00)
　　MS0_P2 [19:0]= \(\displaystyle128 \times 1200 – 1 \times Floor(128 \times \frac{1200}{1})\displaystyle\) = 0
　　MS0_P3 [19:0]= 1
　　R0_DIV[2:0] = 011b（Divide by 8の場合、\(2^3\)）

●その他のレジスター設定

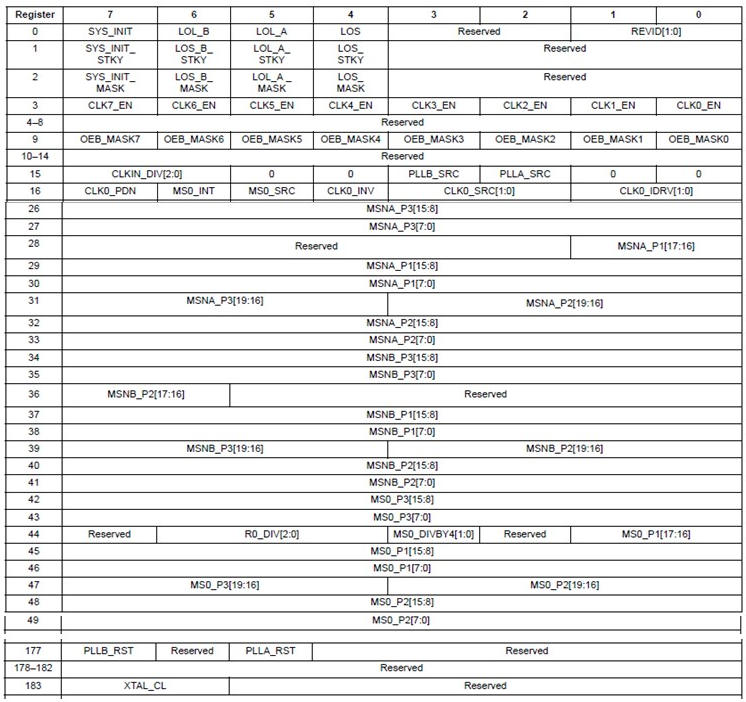
　Reg0 : デバイスのステータス。D7(SYS_INIT)=0の時、Device Ready
　Reg3 : CLK出力の可否。D0(CLK0_EN)=0(CLK0出力可) / 1(不可)
　Reg15 : PLL入力ソース。D4(PLLA_SRC)=0(Select XTAL)
　Reg16 : CLK0 コントロール。
　　　　　D7 : CLK0 Power Down/Up = 0(Powered Up) / 1(Powered Down)
　　　　　D6 : MultiSynth0 Integer Mode = 1 (Integer)
　　　　　D5 : MultiSynth Source Select = 0 (Select PLLA)
　　　　　D4 : Output Clock 0 Invert = 0 (Not inverted)
　　　　　D3-D2 : Output CLK0 Input Source = 11b(Select MultiSynth0)
　　　　　D1-D0 : Drive Strength = 11b(8mA)
　Reg 44 : Multisynth0 パラメータ
　　　　　D6-D4 : 上述R0_DIV[2:0]
　　　　　D3-D2 : MS0 Divide by 4 Enable = 00b(other than 4) 150MHz以下の時
　Reg177 : PLL Reset。　D5(PLLA_RST) = 1(PLLA Reset)
　Reg183 : Crystal Internal Load Capacitance。
　　　　　D7-D6 = 10b(8pF)
　　　　　D5-D0 = 010010b(Reserved)

●レジスター

●Si5351A周波数発生モジュールとプログラムサンプル

・Si5351A周波数発生モジュール(PLLgen5351.py)
パラメータ(a,b,c,A,B,C,R)を設定することで、その周波数を出力する。

# -*- coding: utf-8 -*-
import smbus
import time
import math

I2C = smbus.SMBus(1)
ADR5351 = 0x60		# Si5351A クロックジェネレーター I2C アドレス
DEV_STAT = 0			# Device status
OUT_ENABLE = 3		# Output Enable Cnotrol
PLL_SRC = 15			# PLL Input Source
CLK0_CTL = 16		# Clock0 Control
MULN_PARAM = 26	# Multisynth NA Parameters Start Reg
MUL0_PARAM = 42	# Multisynth0 Parameters Start Reg
XTAL_CL = 183		# Crystal Internal Load Capacitance (8pF) [D7:D6]
PLL_RESET = 177		# PLL Reset

class PLL:
	def __init__(self, freq):
		# freq[no] = [a, b, c, A, B, C, R]
		self.freqNo = len(freq)
		self.MSNA = []
		self.MS0 = []
		for no in range(self.freqNo):
			Fv = freq[no][0:3]		# [a, b, c]
			Fo = freq[no][3:]		# [A, B, C, R]
			self.MSNA.append(self.calcParam(0, Fv))
			self.MS0.append(self.calcParam(1, Fo))
		regData = I2C.read_byte_data(ADR5351, DEV_STAT)		# Device Status
		if regData & 0x80:		# D7 = 0 : Ready
			print("Device Status Error")
			exit(0)
		I2C.write_byte_data(ADR5351, PLL_RESET, 0b10100000)    # PLL Reset
		time.sleep(0.1)
		I2C.write_byte_data(ADR5351, PLL_SRC, 0x00)    # Input Sorce -> XTAL
		I2C.write_byte_data(ADR5351, OUT_ENABLE, 0xFF)    # Disable all clock
		I2C.write_byte_data(ADR5351, XTAL_CL, 0x92)		# Capacitance= 8pF
	
	def calcParam(self, s, p):
		ms = []
		P1 = 128 * p[0] + math.floor(128 * p[1] / p[2]) - 512
		P2 = 128 * p[1] - p[2] * math.floor(128 * p[1] / p[2])
		P3 = p[2]
		ms.append((P3 >> 8) & 0xFF)	# adr=26, 42
		ms.append(P3 & 0xFF)				# adr=27, 43
		r28 = (P1 >> 16) & 0x03			# adr=28
		if s:										# MS0
			for div in range(8):
				if (p[3] >> div) & 1:		# R
					bit = div						# 2^bit
			ms.append((bit << 4) | r28) 	# adr=44
		else:										# MSNA
			ms.append(r28)					# adr=28
		ms.append((P1 >> 8) & 0xFF)	# adr=29, 45
		ms.append(P1 & 0xFF)				# adr=30, 46
		pa, pb = (P3 >> 16) & 0x0F, (P2 >> 16) & 0x0F
		ms.append((pa << 4) | pb) 		# adr=31, 47
		ms.append((P2 >> 8) & 0xFF)	# adr=32, 48
		ms.append(P2 & 0xFF)				# adr=33, 49
		return ms
		
	def freqGen(self, no):
		I2C.write_byte_data(ADR5351, 3, 0xFF)    # Disable All Clock
		I2C.write_byte_data(ADR5351, CLK0_CTL, 0b01001111)    # CLK0 Power Up
		for reg in range(CLK0_CTL+1, CLK0_CTL+8):
			I2C.write_byte_data(ADR5351, reg, 0x80)    # Other Clock Power Down
		I2C.write_i2c_block_data (ADR5351, MULN_PARAM, self.MSNA[no])		# MSNA parameter
		I2C.write_i2c_block_data (ADR5351, MUL0_PARAM, self.MS0[no])		# MS0 parameter
		readData = I2C.read_i2c_block_data (ADR5351, 42, 8)
		I2C.write_byte_data(ADR5351, 3, 0xFE)    # CLK0 Enable
	
	def stopGen(self):
		I2C.write_byte_data(ADR5351, 3, 0xFF)    # Disable clk0

if __name__ == "__main__":
	# 40kHzと60kHzの周波数発生の事例
	freq40 = [15, 1, 1, 50, 1200, 1, 8]		# [a, b, c, A, B, C, R]
	freq60 = [23, 1, 1, 50, 1200, 1, 8]		# [a, b, c, A, B, C, R]
			# F = [a, b, c, A, B, C, R], Fxtal = 25MHz
			# Fvco = Fxtal*(a+b/c) = 25,000kHz*(15+1/1) = 400,000kHz
			# Fvco = Fxtal*(a+b/c) = 25,000kHz*(23+1/1) = 600,000kHz
			# Fout = Fvco/(A+B/C)/R = 400,000/(50+1200/1)/8 = 40kHz
			# Fout = Fvco/(A+B/C)/R = 600,000/(50+1200/1)/8 = 60kHz
			# MSNA40kHz = [0x00, 0x01, 0x00, 0x06, 0x00, 0x00, 0x00, 0x00]		# 40kHz
			# MSNA60kHz = [0x00, 0x01, 0x00, 0x0A, 0x00, 0x00, 0x00, 0x00]		# 60kHz
			# MS040kHz, MS060kHz = [0x00, 0x01, 0x32, 0x6F, 0x00, 0x00, 0x00, 0x00]
	pll = PLL([freq40, freq60])
	pll.freqGen(0)	# 40kHz
	time.sleep(10)
	pll.freqGen(1)	# 60kHz
	time.sleep(10)
	pll.stopGen()