9軸センサーMPU9250へのカルマンフィルタ適用
MPU-9250 9軸センサモジュールは、3軸加速度、3軸ジャイロ、3軸コンパスセンサが1チップに内蔵され、コンパクトでいろいろなアプリケーションに使われている。このブログの中でもラズドローンの姿勢を測定するのに使った。ジャイロの出力値が角速度であるので、数値積分して姿勢角を算出するが、積分計算を含むためドリフト誤差を持つ。一方、加速度はX軸、Y軸、Z軸の加速度の大きさから幾何学的に姿勢角が算出できるがノイズ成分がでてくる。そこで、参考図書「カルマンフィルタの基礎」(足立修一・丸田一郎共著、東京電機大学出版局)のカルマンフィルタの応用としての相補フィルタの適用例を参考にして、姿勢角を精度よく算出できたので、その作成過程を記録に残すことにした。
●使用した9軸センサモジュールMPU-9250
ストロベリー リナックス社販売:価格2,200円(税込)
・InvenSense社(インベンセンス)の9軸センサ MPU-9250をモジュールにしたもので、1チップに3軸加速度、3軸ジャイロ、3軸コンパスセンサが内蔵されている。3軸コンパスセンサは旭化成AK8963。
◇加速度
・測定レンジ ±2 / ±4 / ±8 / ±16g、分解能:16ビット
◇ジャイロ
・測定レンジ ±250 / ±500 / ±1000 / ±2000dps(°/sec)、分解能:16ビット
◇コンパス(AK8963)
・測定レンジ:±4800μT、分解能:14ビット/16ビット
●ラズパイとMPU-9250との接続
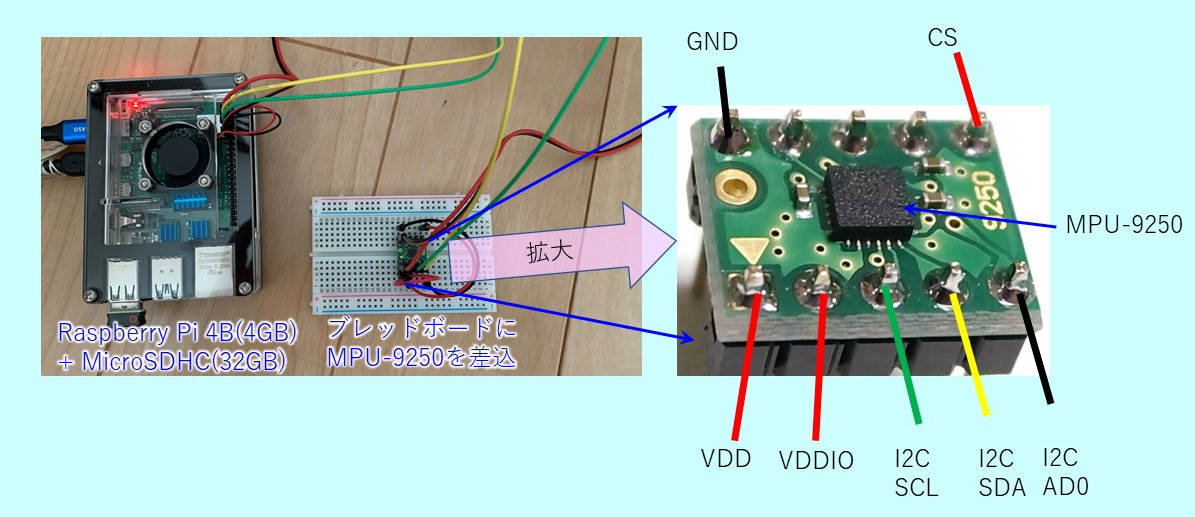
Raspberry Pi 4BとMPU-9250は、CSをVDDIOに接続してI2C接続とした。AD0=LでI2Cスレーブアドレスは0x68とした。
●MPU9250のXYZ軸方向

●MPU9250からのデータ取得プログラム
MPU9250.py
このモジュールを使ったサンプルプログラムでは、単純に加速度、ジャイロ角速度、コンパス磁気を読取り、表示している。
# -*- coding: utf-8 -*-
import smbus
import time
I2C = smbus.SMBus(1) # I2C smbus
MP9250_ADR = 0x68 # MPU9250 I2C slave address
AK8963_ADR = 0x0C # AK8963 I2C slave address
DEVICE_ID = 0x71 ## Device id
# MPU-9250 Register Addresses
SMPLRT_DIV = 0x19
CONFIG = 0x1A
GYRO_CONFIG = 0x1B
ACCEL_CONFIG = 0x1C
ACCEL_CONFIG_2 = 0x1D
INT_PIN_CFG = 0x37
INT_STATUS = 0x3A
ACCEL_OUT = 0x3B
TEMP_OUT = 0x41
GYRO_OUT = 0x43
PWR_MGMT_1 = 0x6B
WHO_AM_I = 0x75
# Gyro Full Scale Index
GFS_250 = 0
GFS_500 = 1
GFS_1000 = 2
GFS_2000 = 3
GYR_FS = [0x00,0x08, 0x10, 0x18] # ジャイロFSレンジのBit設定 Reg29[4:3]
GYR_RNG = [250.0, 500.0, 1000.0, 2000.0] # ジャイロFSレンジ(単位=deg/sec)
# Accel Full Scale Index
AFS_2G = 0
AFS_4G = 1
AFS_8G = 2
AFS_16G = 3
ACC_FS = [0x00, 0x08, 0x10,0x18] # 加速度FSレンジのBit設定 Reg28[4:3]
ACC_RNG = [2.0, 4.0, 8.0, 16.0] # 加速度FSレンジ(単位=G)
# AK8963 Register Addresses
AK8963_ST1 = 0x02 # ステータス
AK8963_MAG_OUT = 0x03 # 測定データ
AK8963_CNTL1 = 0x0A # コントロール
AK8963_ASAX = 0x10 # 感度調整値
# CNTL1 Mode select
AK8963_MODE_DOWN = 0x00 # パワーダウンモード
AK8963_MODE_ONE = 0x01 # 単発測定モード
AK8963_MODE_C8HZ = 0x02 # 連続測定モード1(8Hz)
AK8963_MODE_C100HZ = 0x06 # 連続測定モード2(100Hz)
AK8963_BIT_14 = 0x00 # 14bits output
AK8963_BIT_16 = 0x10 # 16bits output
class MPU9250:
def __init__(self, mpuAdr=MP9250_ADR):
self.mpuAdr = mpuAdr
self.configMPU9250(gfsNo=GFS_250, afsNo=AFS_2G) # Default
self.configAK8963(mode=AK8963_MODE_C8HZ, mfs=AK8963_BIT_16) # Default
def searchDevice(self): # Device Check
who_am_I = I2C.read_byte_data(self.mpuAdr, WHO_AM_I)
if(who_am_I == DEVICE_ID):
return True
else:
return False
def configMPU9250(self, gfsNo, afsNo): # Configure MPU-9250
if gfsNo < 0 or gfsNo > 3:
gfsNo = 3
self.gres = GYR_RNG[gfsNo] / 32768.0
if afsNo < 0 or afsNo > 3:
afsNo = 3
self.ares = ACC_RNG[afsNo] / 32768.0
I2C.write_byte_data(self.mpuAdr, PWR_MGMT_1, 0x00) # sleep off
time.sleep(0.1)
I2C.write_byte_data(self.mpuAdr, PWR_MGMT_1, 0x01) # auto select clock source
time.sleep(0.1)
I2C.write_byte_data(self.mpuAdr, CONFIG, 0x03) # DLPF_CFG(Low Pass Filter 41Hz)
I2C.write_byte_data(self.mpuAdr, SMPLRT_DIV, 0x04) # sample rate divider
I2C.write_byte_data(self.mpuAdr, GYRO_CONFIG, GYR_FS[gfsNo]) # gyro full scale select
I2C.write_byte_data(self.mpuAdr, ACCEL_CONFIG, ACC_FS[afsNo]) # accel full scale select
I2C.write_byte_data(self.mpuAdr, ACCEL_CONFIG_2, 0x03) # A_DLPFCFG(Low Pass Filter 41Hz)
I2C.write_byte_data(self.mpuAdr, INT_PIN_CFG, 0x02) # BYPASS_EN
time.sleep(0.1)
def configAK8963(self, mode, mfs): # Configure AK8963
if mfs == AK8963_BIT_14:
self.mres = 4912.0/8190.0
else: # mfs == AK8963_BIT_16:
self.mres = 4912.0/32760.0
I2C.write_byte_data(AK8963_ADR, AK8963_CNTL1, 0x00)
time.sleep(0.01)
I2C.write_byte_data(AK8963_ADR, AK8963_CNTL1, 0x0F) # set read FuseROM mode
time.sleep(0.01)
data = I2C.read_i2c_block_data(AK8963_ADR, AK8963_ASAX, 3) # read coef data
self.magCoef = [0., 0., 0.]
for ax in range(3):
self.magCoef[ax] = (data[ax] - 128) / 256.0 + 1.0
I2C.write_byte_data(AK8963_ADR, AK8963_CNTL1, 0x00) # set power down mode
time.sleep(0.01)
I2C.write_byte_data(AK8963_ADR, AK8963_CNTL1, (mfs | mode))# set scale&continous mode
time.sleep(0.01)
def checkDataReady(self):
dataReady = I2C.read_byte_data(self.mpuAdr, INT_STATUS)
if dataReady & 0x01:
return True
else:
return False
# Read accelerometer and gyro
def readAccGyro(self):
data = I2C.read_i2c_block_data(self.mpuAdr, ACCEL_OUT, 14)
# ACC=data[0:5], TEMP=data[6:7], GYRO=data[8:13] ---- MSB:LSB
accData = [0., 0., 0.]
for ax in range(3): # set accelerometer data
accData[ax] = self.byte2data(data[ax*2], data[ax*2+1]) # (MSB, LSB)
accData[ax] = round(accData[ax] * self.ares, 3)
gyrData = [0., 0., 0.]
for ax in range(3): # set gyro data
gyrData[ax] = self.byte2data(data[8+ax*2], data[9+ax*2]) # (MSB, LSB)
gyrData[ax] = round(gyrData[ax] * self.gres, 3)
return accData, gyrData
# Read mag
def readMag(self):
magData = [0., 0., 0.]
dataReady = I2C.read_byte_data(AK8963_ADR, AK8963_ST1)
if dataReady & 0x01 : # Check data ready
data = I2C.read_i2c_block_data(AK8963_ADR, AK8963_MAG_OUT, 7)
# MAG=data[0:5] --- (LSB:MSB), OverFlow=data[6]
if (data[6] & 0x08) != 0x08: # Check overflow
for ax in range(3):
magData[ax] = self.byte2data(data[ax*2+1], data[ax*2]) # (MSB, LSB)
magData[ax] = round(magData[ax] * self.mres * self.magCoef[ax], 3)
return magData
# Read temperature
def readTemp(self):
data = I2C.read_i2c_block_data(self.mpuAdr, TEMP_OUT, 2)
tempData = self.byte2data(data[0], data[1]) # (MSB, LSB)
tempData = round((tempData / 333.87 + 21.0), 3)
return tempData
def byte2data(self, byteMSB, byteLSB):
value = (byteMSB << 8) | byteLSB
value = - (value & 0x8000) | (value & 0x7FFF) # 2の補数
return value
if __name__ == '__main__':
mpu9250 = MPU9250(MP9250_ADR) # 0x68
if mpu9250.searchDevice():
print("Who am I? OK")
else:
print("Who am I? Error")
mpu9250.configMPU9250(gfsNo = GFS_2000, afsNo = AFS_16G)
# Full Scale : Gyro=2000deg/sec, Acc=16g
mpu9250.configAK8963(mode = AK8963_MODE_C8HZ, mfs = AK8963_BIT_16)
# mode=Continous 8Hz, 16bit output
for k in range(1000):
if not mpu9250.checkDataReady():
print("Data not ready")
continue
accXYZ, gyrXYZ = mpu9250.readAccGyro()
magXYZ = mpu9250.readMag()
temp = mpu9250.readTemp()
strAcc ="Acc = {:7.2f}, {:7.2f}, {:7.2f}, ".format(accXYZ[0], accXYZ[1], accXYZ[2])
strGyro ="Gyro = {:7.2f}, {:7.2f}, {:7.2f}, ".format(gyrXYZ[0], gyrXYZ[1], gyrXYZ[2])
strMag ="Mag = {:7.2f}, {:7.2f}, {:7.2f}, ".format(magXYZ[0], magXYZ[1], magXYZ[2])
strTemp ="Temp = {:7.2f}".format(temp)
print(strAcc + strGyro + strMag + strTemp)
●カルマンフィルタの計算
カルマンフィルタの導出については、前述の参考図書「カルマンフィルタの基礎」に記載してあり、MATLABのプログラム事例が記載してあるので、ここではその結果だけを使って、pythonプログラムに書き直した。尚、記号もこの参考図書の記述スタイルと同じとした。
多変数時系列データ \(\boldsymbol{y} (k)\)が次の線形離散時間状態空間モデルで記述されると仮定。
\(\begin{eqnarray}
\boldsymbol{x}(k+1) &=& \boldsymbol{Ax}(k) + \boldsymbol {Bv}(k) \\
\boldsymbol{y}(k) &=& \boldsymbol{Cx}(k) + \boldsymbol{w}(k) \\
\end{eqnarray}\)
\(\boldsymbol {A} : n \times n\)行列、\(\boldsymbol {B} : n \times r\)行列、\(\boldsymbol {C} : p \times n\)行列
\(\boldsymbol{y}(k) : p\)次元時系列ベクトル
\(\boldsymbol{x}(k) : n\)次元状態ベクトル
\(\boldsymbol{v}(k) : \)平均値ベクトル\(0、共分散行列\boldsymbol {Q}のr\)次元システム雑音ベクトル
\(\boldsymbol{w}(k) : \)平均値ベクトル\(0、共分散行列\boldsymbol {R}のp\)次元観測雑音ベクトル
<予測ステップ>
事前状態推定値:
\(\boldsymbol{\hat{x}}(k|k-1) = \boldsymbol{A\hat{x}}(k-1)\)
事前誤差共分散行列
\(\boldsymbol {P}(k|k-1) = \boldsymbol {AP}(k-1) \boldsymbol {A^T} + \boldsymbol {BQB^T} \)
<フィルタリングステップ>
カルマンゲイン行列:
\(\boldsymbol {G}(k) = \displaystyle{\frac{\boldsymbol{P}(k|k-1)\boldsymbol {C^T}} {\boldsymbol {CP}(k|k-1) \boldsymbol {C^T} + \boldsymbol {R}}} \)
状態推定値:
\(\boldsymbol{\hat{x}}(k) = \boldsymbol{\hat{x}}(k|k-1) + \boldsymbol {G}(k) \{\boldsymbol{y}(k)\ -\ \boldsymbol{C\hat{x}}(k|k-1)\}\)
事後誤差共分散行列:
\(\boldsymbol{P}(k) = \{\boldsymbol{I} – \boldsymbol{G}(k) \boldsymbol{C}\} \boldsymbol{P}(k|k-1) \)
\(\boldsymbol{\hat{x}}(k|k-1)\) : 時刻\(k-1\)までに利用可能なデータに基づいた時刻\(k\)における\(\boldsymbol {x}\)の事前予測推定値
\(\boldsymbol{\hat{x}}(k) = \hat{x}(k|k)\): 時刻\(k\)までに利用可能なデータを用いた時刻\(k\)において求める\(\boldsymbol {x}\)のフィルタリング推定値
●カルマンフィルタのpythonモジュール
KalmanFilter.py
上述の計算式を、kalmanFilterという関数にした。この関数の引数、戻り値は次の通り。ここで、u(k)は制御入力であるが、今回は使わない。
関数 kalmanFilter(A, B, Bu, C, Q, R, u, y, xhat, P)
引数:
A, B, Bu, C : 対象システム
x(k+1) = A * x(k) + B * v(k) + Bu * u(k)
y(k) = C * x(k) + w(k)
Q, R : 雑音 v, wの共分散行列。v, w は正規性白色雑音
E[v(k)] = E[w(k)] = 0
E[v(k)’v(k)] = Q, E[w(k)’w(k)] = R であることを想定
u: 状態更新前時点での制御入力 u(k-1)
y: 状態更新前時点での観測出力 y(k)
xhat, P : 更新前の状態推定値 xhat(k-1)、誤差共分散行列 P(k-1)
戻り値:
xhat_new: 更新後の状態推定値 xhat(k)
P_new: 更新後の誤差共分散行列 P(k)
G: カルマンゲイン G(k)
# -*- coding: utf-8 -*- import numpy as np def kalmanFilter(A, B, Bu, C, Q, R, u, y, xhat, P): ## 予測ステップ nn = A.shape[0] #事前状態推定値 xhat_m = A @ xhat + Bu @ u # 事前誤差共分散行列 P_m = A @ P @ A.T + B @ Q @ B.T ## フィルタリングステップ #カルマンゲイン行列 G = P_m @ C.T / (C @ P_m @ C.T + R) # 状態推定値 xhat_new = xhat_m + G @ (y - C @ xhat_m) # 事後誤差共分散行列 I = np.eye(nn) P_new = (I - G @ C) @ P_m return xhat_new, P_new, G
●相補フィルタを用いた傾き角の計算
ジャイロセンサの測定誤差\(e_{1}(k)\) は、1次低域通過フィルタ\(\mu(k)\) とバイアス成分\(\beta(k)\) を用いて次の式で記述できる。
\(e_{1}(k) = \mu(k) + \beta(k)\)
ただし
\(\mu(k+1) = a\mu(k) + (1-a)v_{1}(k), \mu(0) = \mu_{0}\)
\(0 < a < 1\)
\(v_{1}(k)\) : 平均値\(0\)、分散\(\sigma^{2}_{v_1}\)の正規性白色雑音
\(\beta(k+1) = \beta(k), \beta(0) = \beta_{0}\)
加速度センサの測定誤差\(e_{2}(k)\)は、
\(e_{2}(k)\ =\ v_{2}(k-1)\)
\(v_{2}(k):平均値0\)、分散\(σ^{2}_{v_2}で、v_{1}\)と独立した正規性白色雑音。
2つのセンサ出力\(y_{1}(k), y_{2}(k)\)は、真値を\(z(k)\)とすると、
\(\begin{eqnarray}
y_{1}(k) &=& z(k) + e_{1}(k)\\
y_{2}(k) &=& z(k) + e_{2}(k)\\
\end{eqnarray}\)
相補フィルタの観測方程式は
\(\begin{eqnarray}
y(k)&=&y_{1}(k)\ –\ y_{2}(k)\\
&=& e_{1}(k)\ –\ e_{2}(k)\\
&=& \mu(k) + \beta(k)\ –\ e_{2}(k)\\
&=& \boldsymbol {cx}(k)
\end{eqnarray}\)
ここで
\(\boldsymbol {c} = \left[\array{1&1&-1}\right]\) \(\boldsymbol{x}(k) = \left[\array{\mu(k)\\\beta(k)\\e_{2}(k)}\right]\)
状態推定値\(\hat{x}(k)\)からそれぞれのセンサ測定誤差は
\(\begin{eqnarray}
\hat{e_{1}}(k) &=& \hat{x_{1}}(k) + \hat{x_{2}}(k)\\
\hat{e_{2}}(k) &=& \hat{x_{3}}(k)
\end{eqnarray}\)
補正された測定値\(\hat{y}(k)\)は次の式から求められる。
\(\begin{eqnarray}
\hat{y}(k) &=& y(k)\ -\ \hat{x_{1}}(k)\ -\ \hat{x_{2}}(k)\\
\hat{y}(k) &=& y(k)\ –\ \hat{x_{3}}(k)
\end{eqnarray}\)
計算には次のパラメータ、初期値を用いた。
\(\boldsymbol {A} = \left[\array{a&0&0\\0&1&0\\0&0&0}\right]\) \(\boldsymbol {B} = \left[\array{1-a&0\\0&0\\0&1}\right]\) \(\boldsymbol {P}(0) = \left[\array{1000&0&0\\0&1000&0\\0&0&1000}\right]\)
\(\boldsymbol {Q} = \left[\array{60&0\\0&60}\right]\) \(R = 10^{-4}\)
●カルマンフィルタを用いた傾き角の算出プログラム
getAngle.py
MPU9250からジャイロ、加速度データを読み出し、カルマンフィルタを通して補正した角度データを出力する。
このプログラムでは、データをテキストデータとしてファイルに保存
# -*- coding: utf-8 -*-
import MPU9250 as MP
import time
import math
import KalmanFilter as KF
import numpy as np
mpu9250 = MP.MPU9250(MP.MP9250_ADR) # 0x68
if not mpu9250.searchDevice():
print("Who am I? Error")
exit(1)
mpu9250.configMPU9250(gfsNo = MP.GFS_2000, afsNo = MP.AFS_16G)
# Full Scale : Gyro=2000deg/sec, Acc=16g
mpu9250.configAK8963(mode = MP.AK8963_MODE_C8HZ, mfs = MP.AK8963_BIT_16)
# mode=Continous 8Hz, 16bit output
def main():
global preTime, preXdegS, preYdegS, preZdegS
global xDegSum, yDegSum
global xhat_k, yhat_k, xnP, ynP
if not mpu9250.checkDataReady():
return ""
[accX, accY, accZ], [gyroX, gyroY, gyroZ] = mpu9250.readAccGyro()
gyroX += gyroOffX
gyroY += gyroOffY
gyroZ += gyroOffZ
# Gyro 角速度の積分
nowTime = time.time()
dT = nowTime - preTime
xDegSum = xDegSum + (preXdegS + gyroX) / 2.0 * dT
yDegSum = yDegSum + (preYdegS + gyroY) / 2.0 * dT
preXdegS, preYdegS = gyroX, gyroY
preTime = nowTime
# 加速度から角度算出
xDegAcc = math.degrees(math.atan(accY / math.sqrt(accX * accX + accZ * accZ)))
yDegAcc = math.degrees(math.atan(-accX / math.sqrt(accY * accY + accZ * accZ)))
# Kalman Filterによる補正(X軸、Y軸)
xDeg = np.array([[xDegSum - xDegAcc]])
yDeg = np.array([[yDegSum - yDegAcc]])
# 時間更新
xhat_k, xnP, G = KF.kalmanFilter(matA, matB, matBu, matC, matQ, nR, u, xDeg, xhat_k, xnP)
yhat_k, ynP, G = KF.kalmanFilter(matA, matB, matBu, matC, matQ, nR, u, yDeg, yhat_k, ynP)
# 推定値を用いて各センサ出力を補正
xDeghat1 = xDegSum - xhat_k[0] -xhat_k[1]
yDeghat1 = yDegSum - yhat_k[0] -yhat_k[1]
dataStr = " {:10.4f}, {:10.4f}, {:10.4f}, {:10.4f}, {:10.4f}, {:10.4f}, {:10.4f}, {:10.4f}, {:10.4f}"\
.format(nowTime - timeStart, xDegAcc, xDegSum, gyroX, xDeghat1[0], yDegAcc, yDegSum, gyroY, yDeghat1[0])
return dataStr
# Gyro Offset
gyroOffX = 0.121
gyroOffY = -0.171
gyroOffZ = 0.0
# Initial Data
xDegSum, yDegSum = 0.0, 0.0
preXdegS, preYdegS = 0.0, 0.0
preTime = time.time()
timeStart= preTime
# Kalman Filter Parameter
a = 0.75
matA = np.array([[a, 0, 0], [0, 1, 0], [0, 0, 0]])
matB = np.array([[1-a, 0], [0, 0], [0, 1]])
matBu = np.array([[0]])
matQ = np.array([[60, 0], [0, 60]])
nR = 1e-4
matC = np.array([[1, 1, -1]])
u = np.array([[0]])
xhat_k = np.array([[0.], [0.], [0.]])
yhat_k = np.array([[0.], [0.], [0.]])
xnP = np.eye(3) * 1000 # 誤差共分散
ynP = np.eye(3) * 1000 # 誤差共分散
fname = "degdata.txt"
fp = open(fname, 'w')
while True:
try:
dataStr = main()
if len(dataStr) > 0:
fp.write(dataStr+"\n")
except KeyboardInterrupt:
break
fp.close()
●カルマンフィルタを通した計算結果
(1)ジャイロ読取りデータのオフセット量
センサーを傾きの無い場所に置いた時に、ジャイロデータの読み取り値がゼロにならないので、読み取り値に対するオフセット量を設定した。
<ジャイロ読取り値(オフセット無し)>
ジャイロデータ(deg/sec)がゼロ点からズレているので、積分値(deg)は大きく変化している。
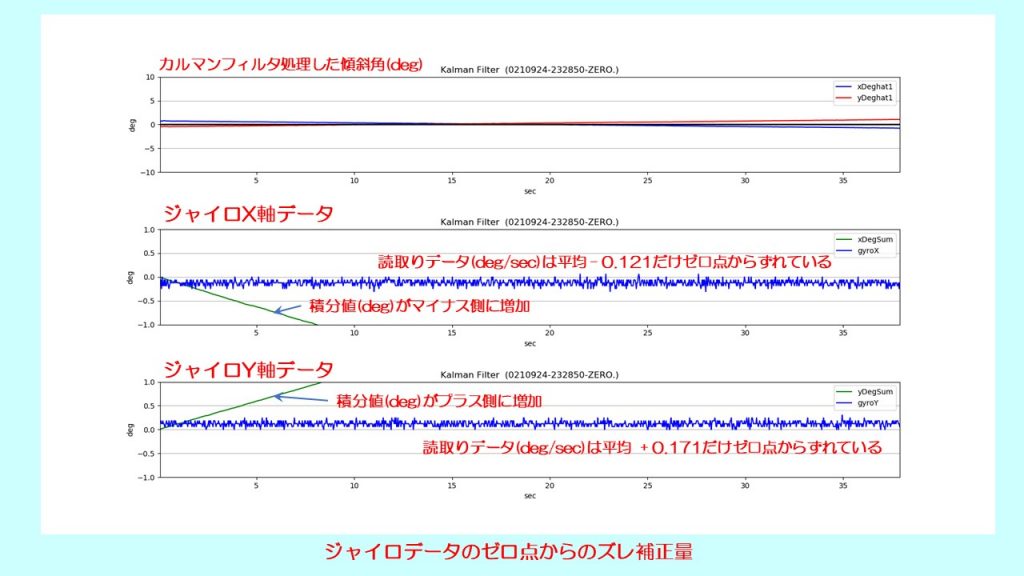
<ジャイロ読取り値(オフセット補正後)>
ゼロ点からのズレ量、X軸:-0.121、Y軸:0.171を補正した結果、読取り値はほぼゼロ点付近となり、積分値(deg)の大幅な変化はない。

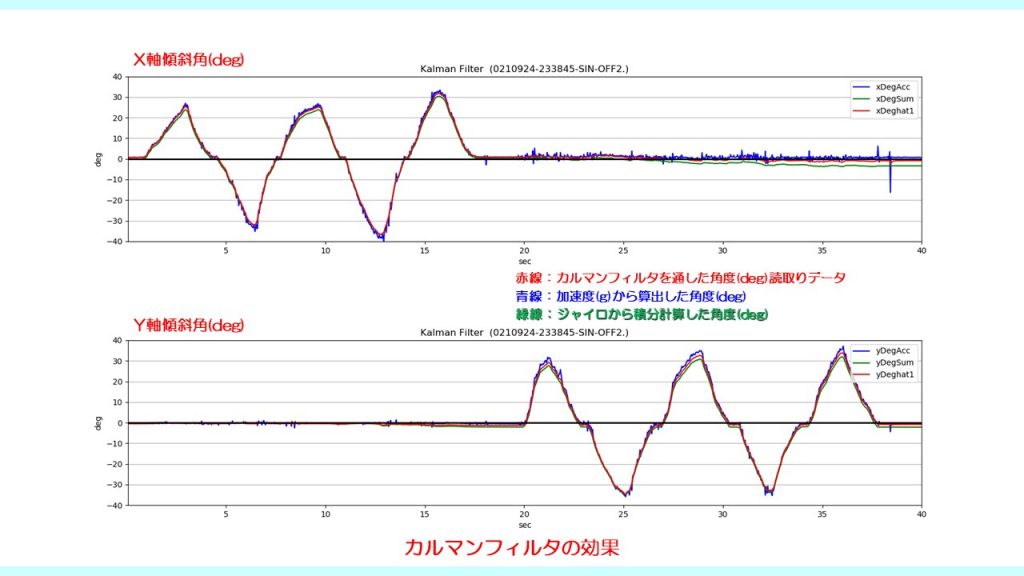
(2)カルマンフィルタの効果
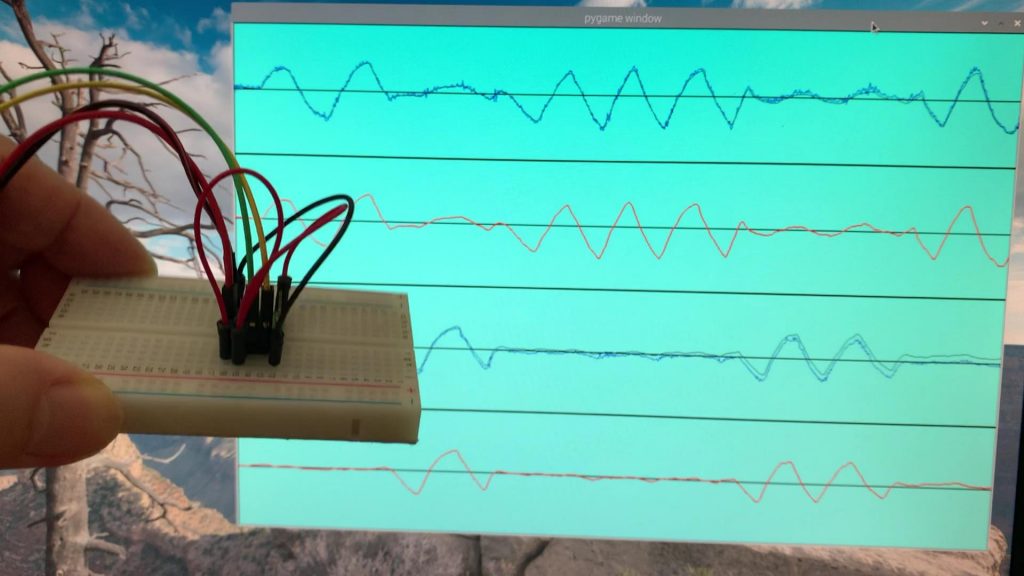
カルマンフィルタを通した角度データ(赤色線)はジャイロ積分データ(緑色線)のドリフトや、加速度から計算した角度データ(青色線)のノイズの影響を排除したデータとなっている。
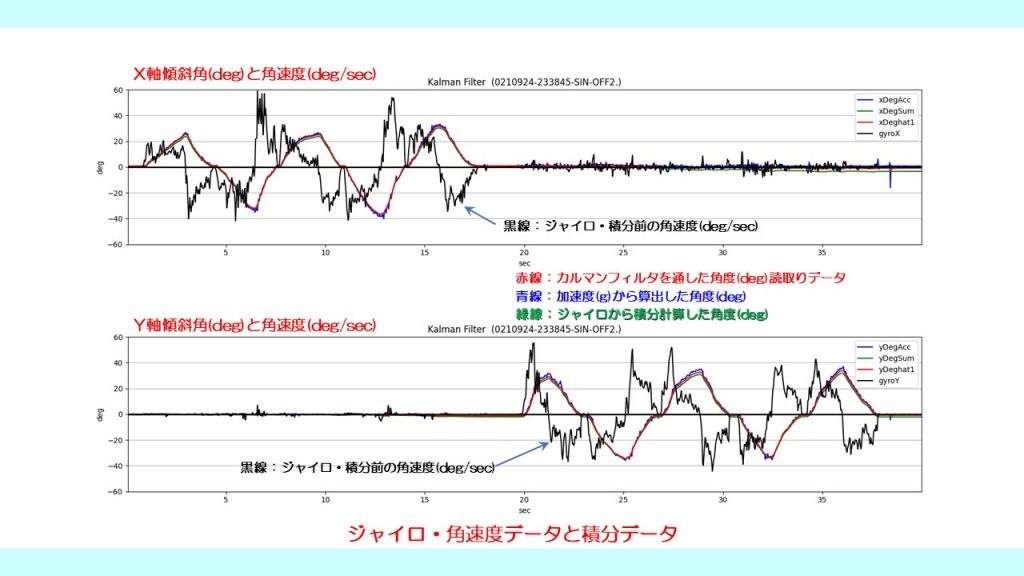
<ジャイロの角速度と積分データ>
ジャイロの角速度データ(黒線)と積分データ(緑線)をプロットした。角速度は高い周波数で変化している。サンプリング周期は5msec.
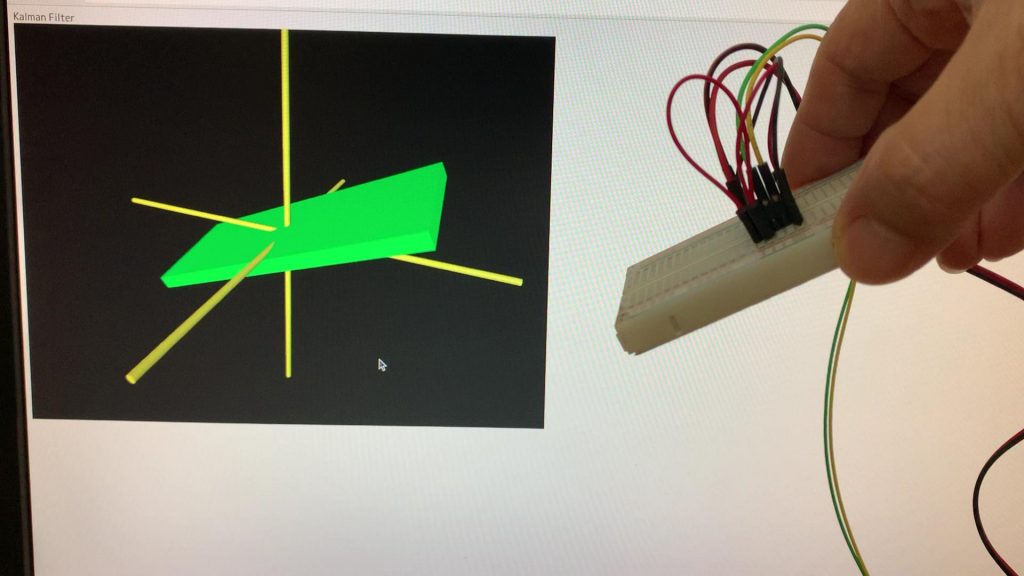
●MPU-9250-9軸センサの傾きを3D描画
カルマンフィルタを用いた相補フィルタを適用して、姿勢角を得て、3D表示。3D表示はVPythonを使った。
●MPU-9250-9軸センサの傾きをグラフ表示
ジャイロの角速度と加速度から算出した傾斜角と、カルマンフィルタを通して補正した傾斜角をグラフ表示した。グラフはpygameを使って描画。